Design

Circular assembly is to construct size-determined homomultimer. The dihedral angle between stacking surfaces determines the number of stacking (Fig. 1). Concretely speaking, the number of stacking is given by

\[{N_c}=(\frac{360°}{α}) \tag{1} \]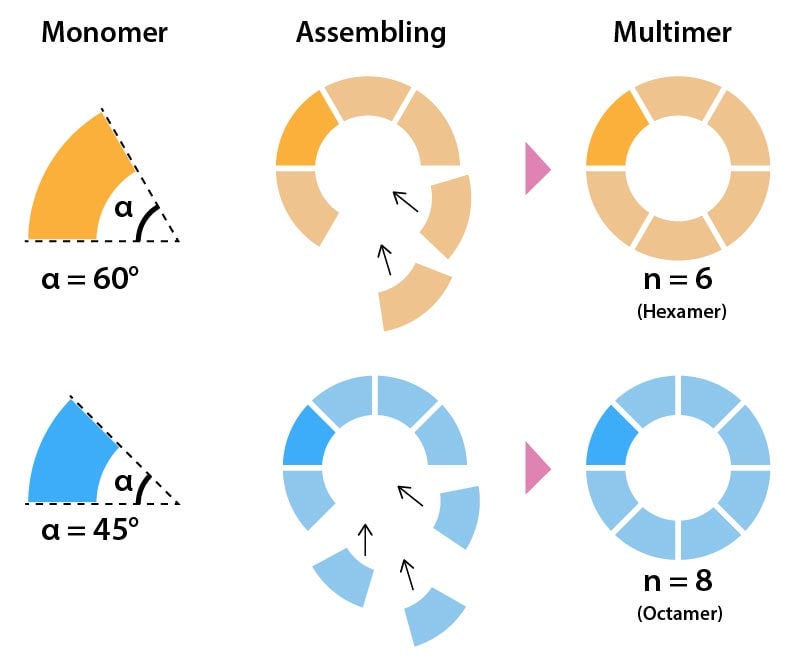

This principle is based on the fact that a ring is a connected shape with no end points. However, this principle is not possible to apply to a linear assembly. Here, we propose a novel method to control linear homomultimers based on geometrical constraints.

To this end, we introduced a vernier mechanism consisting of a hollow cylinder (blue) and a twisted shaft (red), where the shaft can rotate inside the cylinder (Fig. 2).

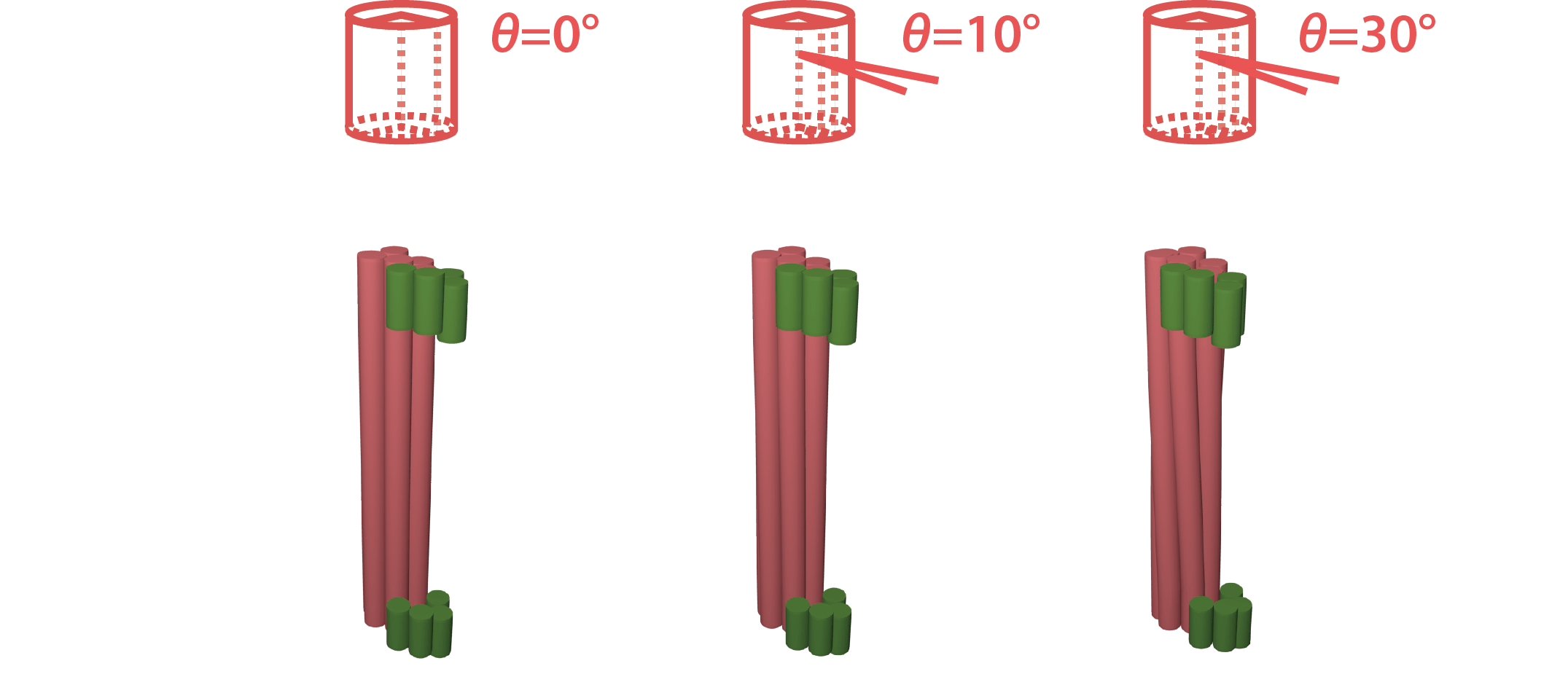
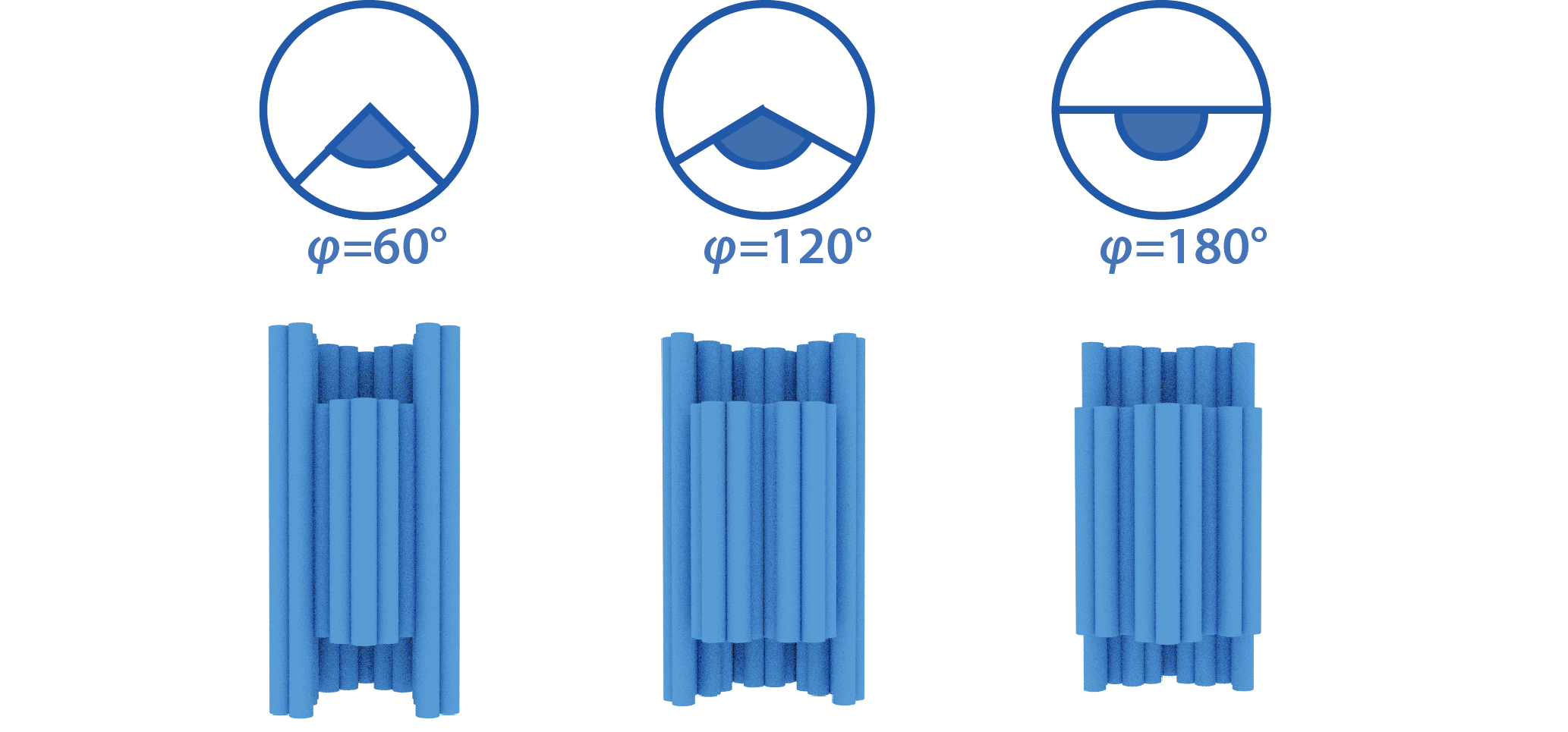
Since the shaft is slightly twisted, there is a phase shift θ between the top and bottom ends. The grooves on the cylinder limit the rotation of the shaft within a particular range φ. Therefore, the shaft can move within the range of φ-θ. As the monomers stack, the phase shift accumulates on the shaft in proportion to the number of stacking n. When the accumulated twist on the shaft reaches the limit of the range, the monomer cannot stack any more (Fig. 3).

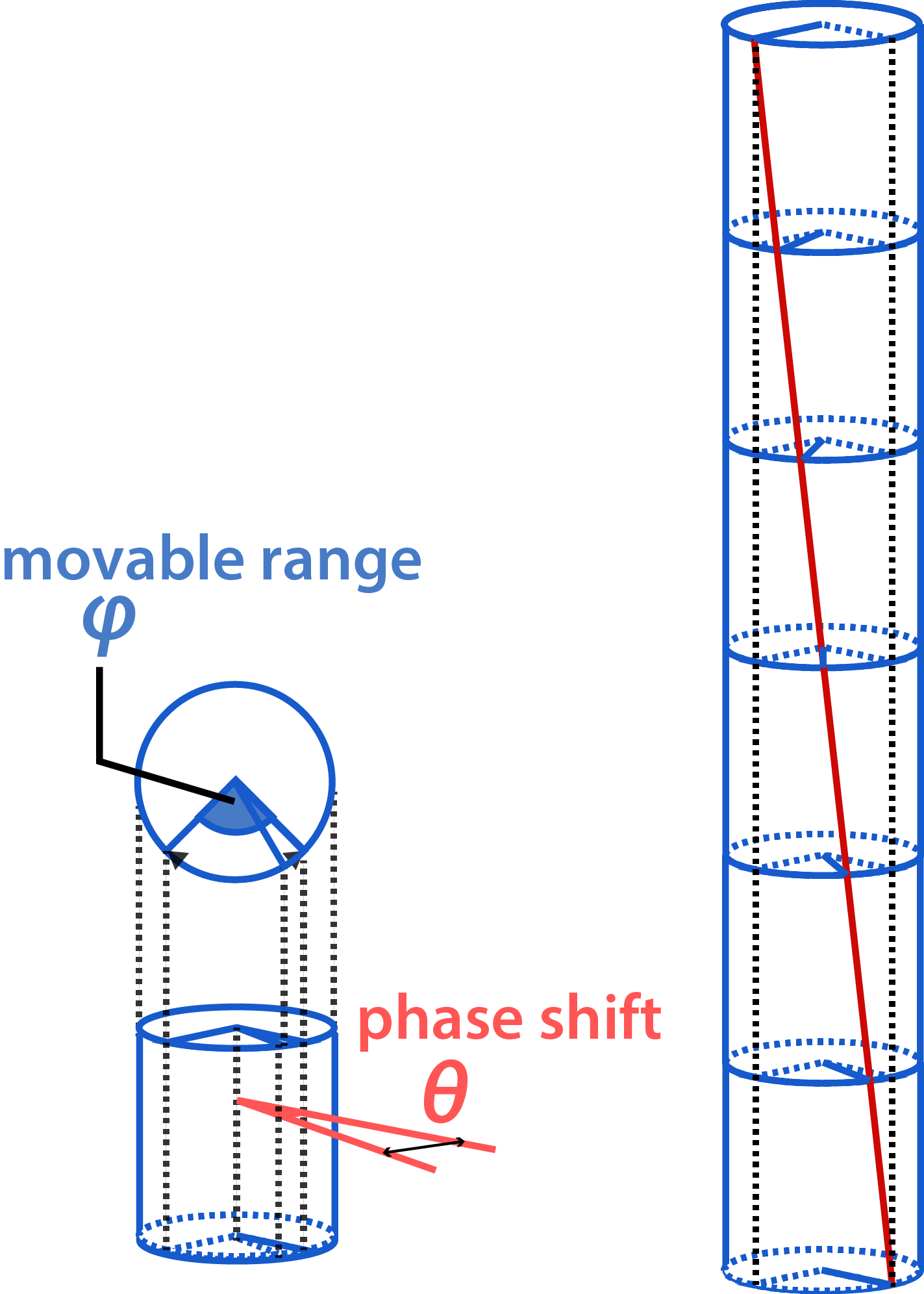
The number of stacking monomers is restricted as follows:

\[n≦\frac{φ-θ}{θ} \tag{2} \]

Therefore, the maximum number of stacking monomer is given by

\[{N_l}=\lfloor \frac{φ-θ}{θ}\rfloor \tag{3} \]

where \(N_l\)is the largest integer less than \(\frac{φ-θ}{θ}\)

Note that we can control the number of stacking by adjusting the twist angle θ and the range of the groove φ.

In order to realize the concept, we designed the monomer by DNA origami (Fig. 4) inspired by previous structure [1]. The shaft consists of a rod and two heads on its both ends. The rod is made of 6 double helices (6 helix bundle, 6HB) while the heads are made of 4 helices. The shaft is twisted by adjusting the interval distance among the crossovers in the 6HB. The cylinder is made of 30 double helices. 12 of them are shorter than others so as to make rotating space (groove) for the head. This special shape can determine the movable range of the shaft. We set the twist angle θ to be 10°[2] and the movable range φ to be 120°. According to Equation (3), the maximum stacking number should be 11.

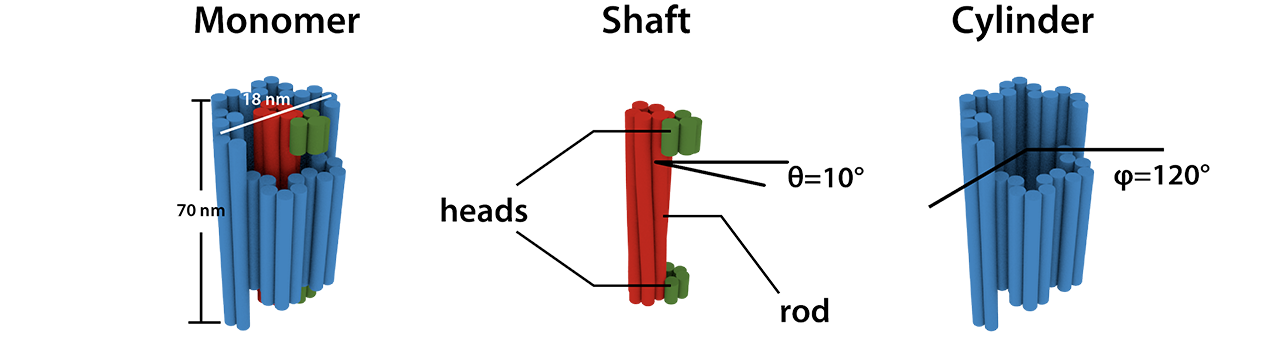
Instead of sticky end hybridization, we use shape-complementary blunt ends [3]. The monomer can stack each other only when the shape-complementary surfaces on both the cylinder and the shaft matches in the pre-determined way (Fig. 5).

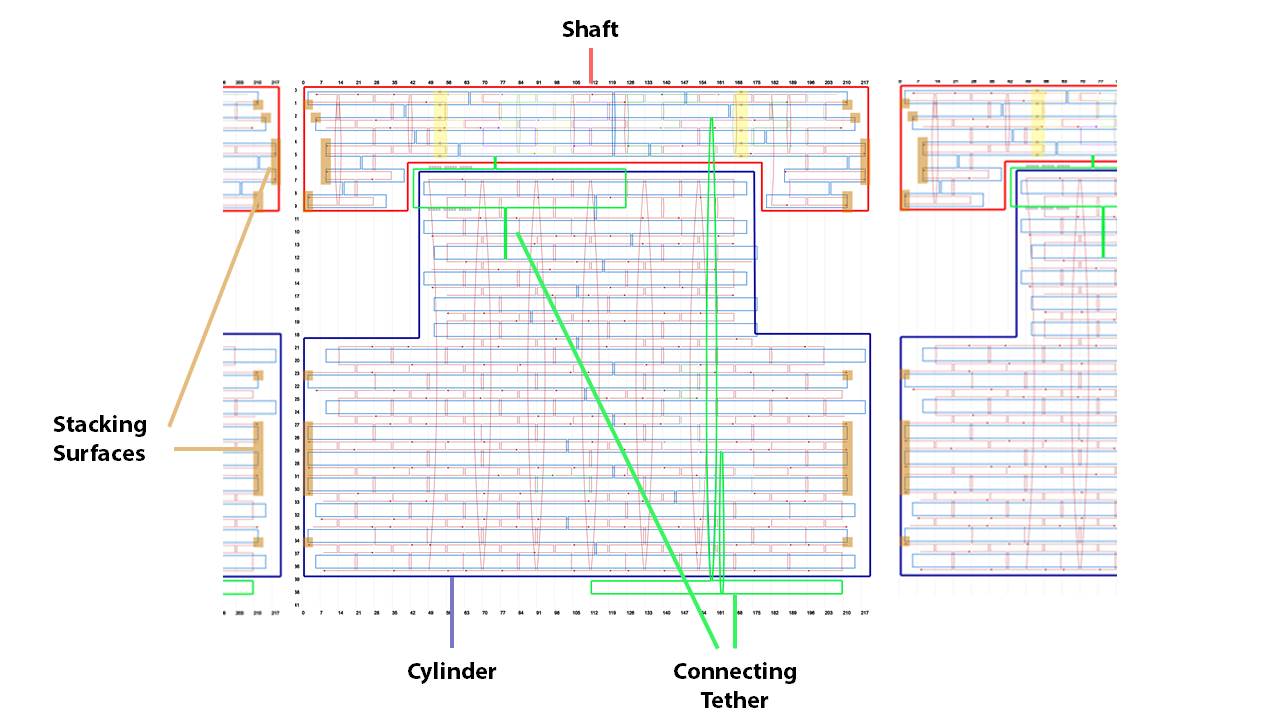
The DNA origami is designed by caDNAno2 [4] (Fig. 6). M13mp18 is used as the scaffold. The staples of the shaft are longer than those of the cylinder to set the melting temperature of the shaft higher than that of the cylinder. During annealing, the shaft forms first, then the cylinder surrounds the shaft.

These shaft and cylinder are made from one scaffold. To avoid undesired entanglements, the shaft is tethered to the cylinder at two points, one is close to the top and the other is close to the bottom.

According to Equation (3), the number of stacking is determined by the twist angle θ and the movable range φ. In 3D DNA origami, twisting of the structure can be induced by skipping or inserting base pairs between crossovers [2].

In our design, by skipping 1 base, the shaft twists clockwise in 5°, while it twists counter clockwise in the same angle by inserting 1 base (Fig. 7). To adjust the twist angle θ, a certain number of bases are skipped or inserted properly. In the following experiment, we use the shaft with 10° twist by skipping 2 bases.

To adjust the movable range φ, which is determined by the groove shape of the cylinder, we can make different movable ranges by adding/deleting the staples, such as 40°, 60°, 80°, 100°, 120°, 160°, 180°, 220°, 240° (Fig. 8).